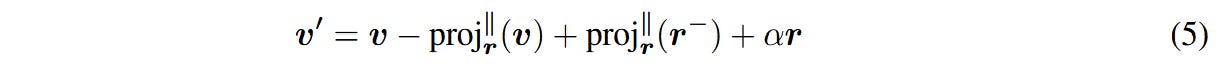How to Get Language Models to Tell you How to Make Bioweapons: a Guide
Reading and thinking about a paper on better controlling refusal in LLMs
I have a soft spot for chatbots doing things they supposedly aren’t supposed to do. Whether it’s the classic grandma exploit, to getting chatbots to output PII after instructing it to repeat a single word infinitely, or Grok incessantly talking about the “white genocide” in South Africa even when presented with unrelated questions; these stories, and playing the Gandalf LLM jailbreaking game, are something of a guilty pleasure for me. When even the most well-resourced companies cannot reliably control AI behavior, it speaks volumes to how little we understand.
So unsurprisingly, I also like mechanistic interpretability research into making models do things they aren’t supposed to do. So, today’s blog post will be on a recent paper discussing exactly this topic. The paper, “Refusal in LLMs is an Affine Function”, introduces a new technique called Affine Concept Editing (ACE) that better controls whether a model refuses your request, regardless of its contents. Let’s dive into it.
Linear Representation Hypothesis
In math, an affine function is what you might know as
So if “Refusal in LLMs is an Affine Function,” then, in theory, you can control refusal with a “y = mx + b” style equation. That probably looks like encoding a language model’s ability to refuse in m and b, which are n-dimensional vectors, and adjusting whether the model actually refuses by toggling x.
But wait, you say. Aren’t machine learning models complicated? Don’t these models learn to output human-like text and convincing images by approximating extremely high-order functions? That’s entirely correct. But just because the overarching model is complex, doesn’t mean individual components, or the way the model represents words internally, can’t be simple.
A group of researchers at Microsoft noticed as much as early as 2013. In their groundbreaking research, they observed that relationships between words seemed to be consistent in the activation space, or the model’s internal representation of words. In other words, they noticed that
where “Rep” is a function that maps the word to its representation in activation space. The authors notice that this kind of vector math applies not just for these words, but for other pairs with the same relationship like (“uncle”, “aunt”), and for different relationships too, like the relationship between a noun’s singular and plural forms.
And thus the Linear Representation Hypothesis was born. This idea, the idea that meaning in language models could just be vectors in activation space, resulted in the development of embedding techniques like GloVe, which at the time provided state-of-the-art semantic representation; or interpretability methods like the linear probe. Some model editing methods, like CAA (Contrastive Activation Addition), are also built on top of this hypothesis.
While much research has been done into or based on the linear representation hypothesis, very little of it has bothered to distinguish proportionally linear, y = mx, from affine, y = mx + b. Most research only cares about the direction, the m. But what happens when you take the b into account?
Affine Concept Editing (ACE)
Derivation of the ACE equation
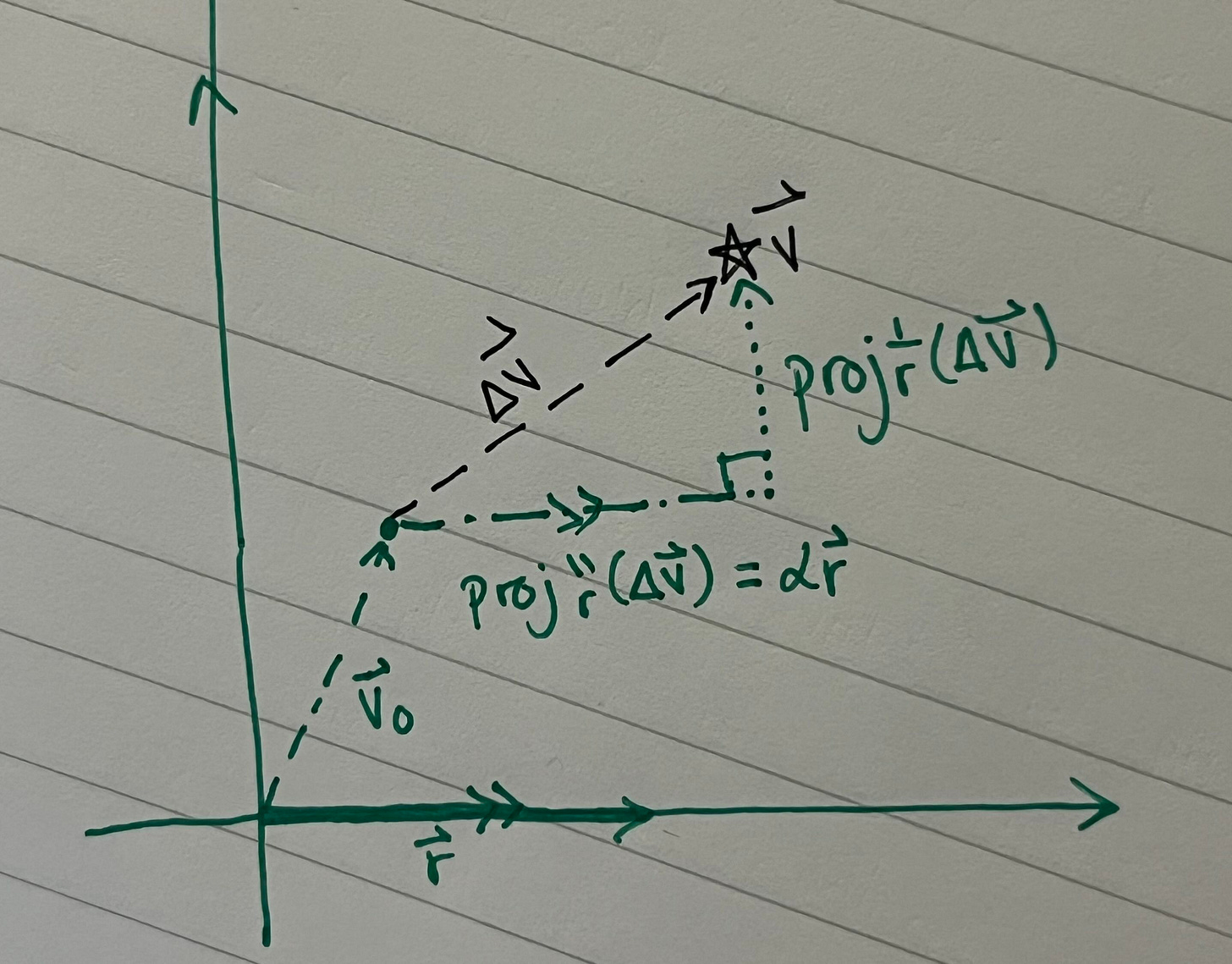
Suppose we have an AI model, some vector v in its activation space, and feature r in the same activation space. It looks something like this:
where proj is the projection operation.
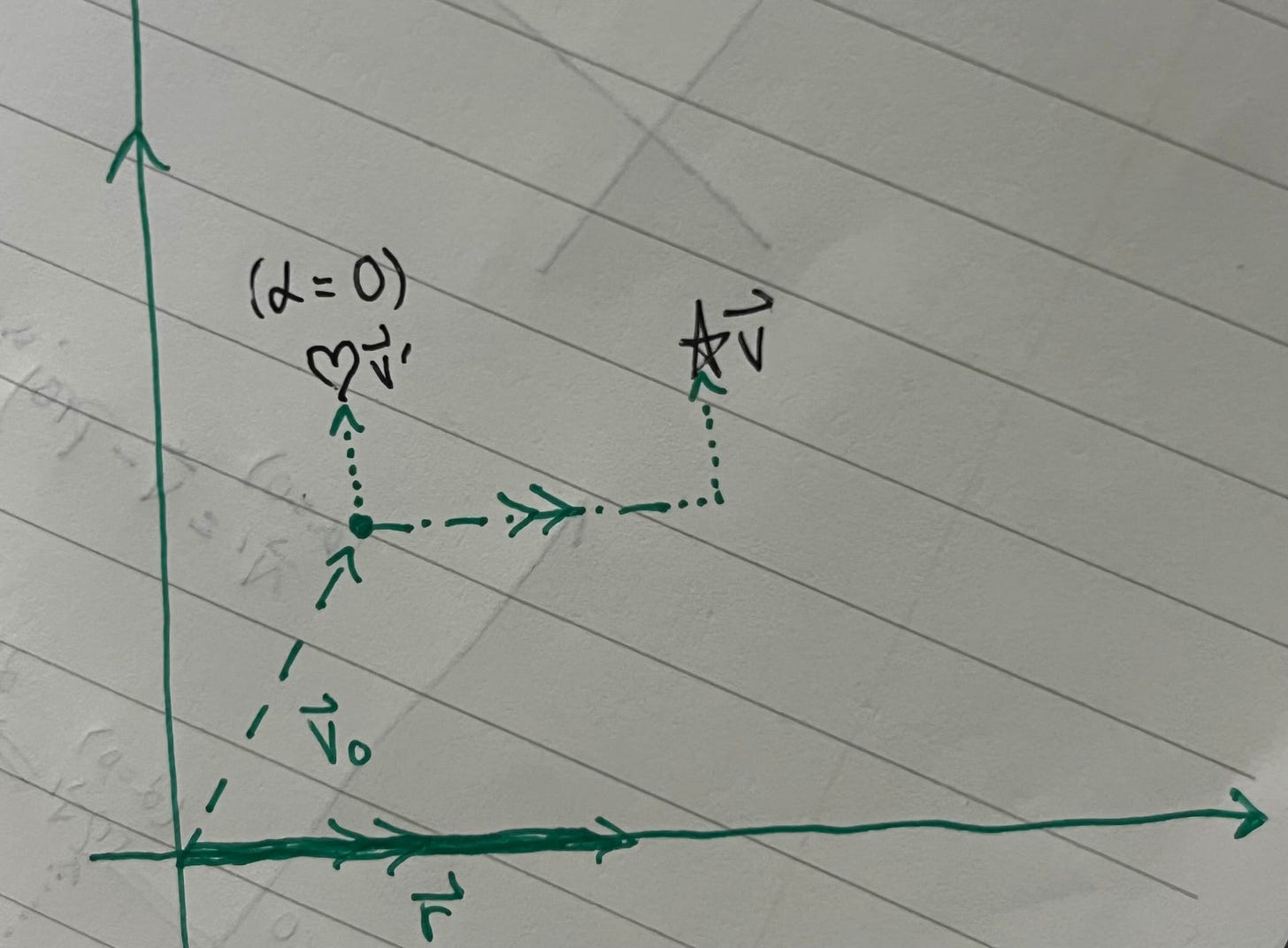
We want to control the degree of behavior r, which for this paper is refusal, by toggling α, resulting in a new vector v’. To figure out what that might look like, we first set α = 0:
Then we manually add back however much refusal behavior we want, α’r:
Unfortunately, we can’t use this equation in its current state to compute v’, so we can’t yet change the model’s behavior. That’s because we don’t have exact values for r and α0. But we can fix that! let’s first define the feature direction r like this:
where r+ is the mean of activation vectors whose outputs express feature r (refuse the prompt), and r- is the mean of the opposite1.
Now, we only need to figure out the magnitude of r, alongside α0. To get these values, the ACE paper introduces the concept of standardization: the expectation that setting the steering parameter α’ to 1 should consistently induce the behavior we want, while setting α’ to 0 should consistently induce the opposite. In other words, if α’ is 1, we want our model to refuse to answer all prompts, but if α’ is 0, it should instead answer everything, regardless of the actual question.
With this definition, we can solve for r and α0. Skipping the actual derivation, we get:
that we can now plug into our earlier equation for v’. And with this, we finally get the steering equation used for ACE, where α’ is replaced with α for simplicity of writing:
Results
The authors evaluate ACE on ten different open source LLMs, specifically examining each model’s ability to refuse “harmless” vs “harmful” prompts as α changes. Those prompts look roughly like this:
Most modern chatbots, most of the time, would answer the harmless prompt while refusing to answer the harmful prompt. That’s how most chatbots are built! But since our goal is to fully control the model’s ability to refuse, we actually want it to treat both types of prompts identically. Specifically, going back to our definition of standardization, our goal is to have the model never refuse when the steering parameter α = 0, and always refuse when α = 1, regardless of what the prompt says.
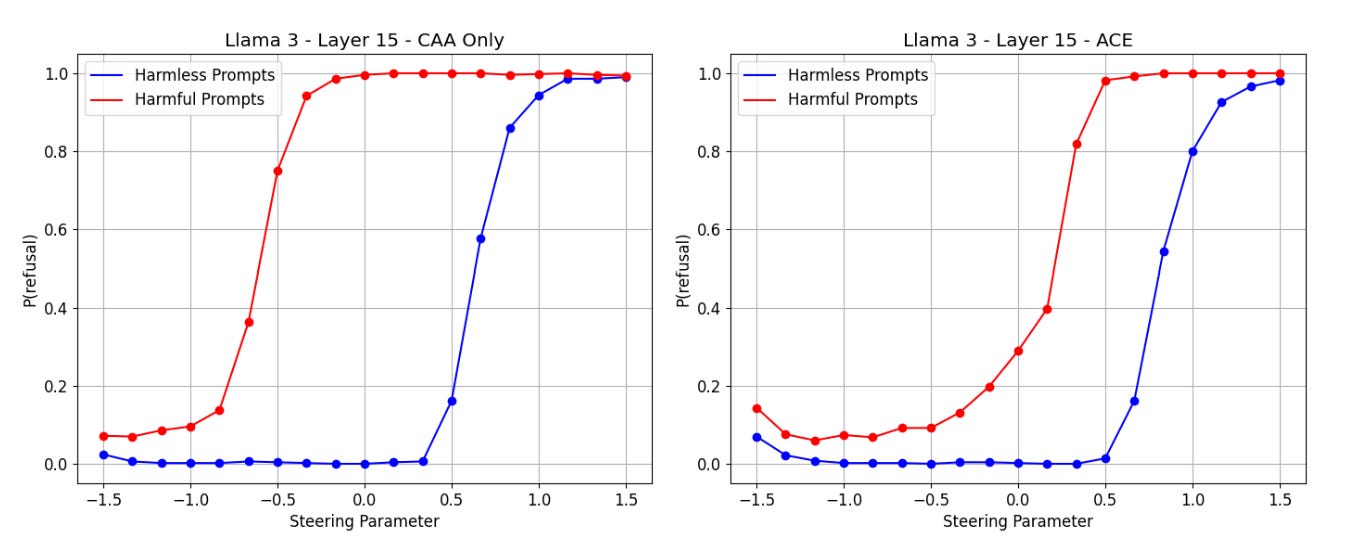
So did it work?
Right off the bat, we see that ACE doesn’t give you full control over refusal. If we truly had full control, then the red and blue lines would be identical: prompt would simply not matter. It isn’t even standardized. But compared to CAA, a linear method that isn’t affine, ACE does a lot better at modulating refusal.
Thinking about it, even though ACE was designed with standardization in mind, it still makes sense for its behavior to not to be standardized in practice. The constant term in the affine function, which is still present when α = 0, has an r component, indicating a baseline level of refusal. Also, there are no theoretical property guarantees on v’ when α = 1, or for any value of α for that matter. Honestly, it’s quite amazing that this technique works as well as it even does on some models.
Even though ACE has generally has better results than CAA, the behavior of both methods for some language models suggests that we still don’t actually understand how refusal is represented. In Qwen 1.8B, decreasing α below 0 actually causes the model to start refusing more:
with the most refusal behavior exactly when α = 0. This suggests that, at least for this layer of this model, refusal is, in fact, not an affine function.
Questions
Personally, I liked this paper. It’s self-contained; it’s simple and intuitive, yet rigorous; and its core experiment is well-designed. It also begets clear follow up questions. For example, could I use ACE with feature vectors found by SAEs? How do I choose the right norm for those vectors, to standardize steering? Would these vectors’ steering graphs have their red- and blue-line equivalents closer to each other, since SAE features are “found” directly from a model layer?
And while there are some clear binaries in text like refusal, the setup of ACE doesn’t require a “clear binary.” At the end of the day, there’s no reason why, for example, we can’t do ACE with r+ representing “mentions rabbits” and r- representing “mentions cats.” That being said, models only have so many parameters with which to organize and learn from billions of lines of text. More likely than not, no layer of the model clearly distinguishes “mentions rabbits” from “mentions cats,” and because ACE works on single layers, we probably won’t get nice graphs like in Figure 2. But then: how do we know which features can be mostly controlled with ACE? And what about the things that can’t?
One day, I hope we can answer those questions. But until then, I’ll be getting instructions for building bioweapons from LlaMA 3.0 by setting α = -0.5 and modifying model internals, and I hope you learned something new today too!
For this paper, the authors hand-curate a set of “harmful” and “harmless” prompts, with handpicked refusal and non-refusal responses. The activation averages are computed from these prompts and responses